私自信、平面上に絵をかく自信がありません。(^^;; で、困ったなあと思っていたところ、何と!まるケンさんが、3D見取り図を作成してくれました。赤と青の立体メガネがあれば感動的な見取り図を見ることができます。まるケンさん、本当にありがとうございました!m(__)m
さて、この問題を解くコツは、完成した立体をきちんと「分析」することです。で、まずは完成した立体が上下対称であることに注目します。つまり、上半分か下半分の立体の体積を求めればあとはそれを2倍すればよい、ということになるわけですね。というわけで、下の図のようにもとの平行四辺形を2分割してみることにします。
さて上図の平行四辺形の上半分だけについて考えてみます。これを270゜回転させると下のような立体ができあがります。
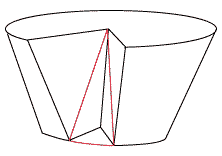
この立体は、半径6cm、高さ8cmの円すい(以下、“円すい”)から作られた(というか、切りとられた)2つの部品で構成されています。 1つは上の図の赤い部分ですね。これは、“円すい”をちょうど半分の高さで底面と平行な平面で切ったときの上半分の4分の1の立体です。(中心角が90゜であることに注意)つまり、その体積は、
6×6×3×8÷3×1/8 × 1/4 =9cm3
 ̄ ̄ ̄ ̄ ̄  ̄ ̄ ̄  ̄ ̄ ̄
(底面の面積) (上の部分)(中心角90゜)
もう一つは上の図のその他の部分ですね。これは、“円すい”をちょうど半分の高さで底面と平行な平面で切ったときの下半分の4分の3の立体です。(中心角は270゜ですね)つまり、その体積は、
6×6×3×8÷3×7/8 × 3/4 =189cm3
 ̄ ̄ ̄ ̄ ̄  ̄ ̄ ̄  ̄ ̄ ̄
(底面の面積) (下の部分)(中心角270゜)
あとはこれを合計して、2倍すればでき上がりですね。
(189+9)×2=396
答え:396cm3