説明の非常に難しい問題ですね。（^_^;　

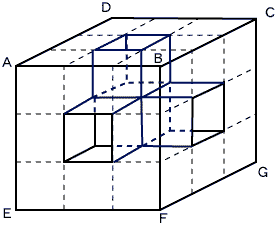
　とりあえず、上の２つの図をご覧ください。

　考え方はさまざまなのですが、ここでは立方体ＡＢＣＤーＥＦＧＨを３×３×３＝２７個の小さな立方体の集まりと考えることにします。左の図は、それを（多少）分かりやすく書いたものです。右の図は、それを切ったところを図示したものです。

　さて、立方体ＡＢＣＤーＥＦＧＨの切り方ですが、切り口の図形が（もし空洞なければ）正三角形になります。これは切られる小さい立方体にも言えることです。（同じ角度で切るわけですから....）例えば、頂点Ａを含む小さな立方体をご覧いただければ比較的簡単に想像できると思います。

　あとは、切られ方を考えるだけです。ＡＣ、ＡＦ、ＣＦの３辺はそれぞれ３等分されています。なぜなら、それぞれの辺は小さい立方体の対角線３つ分だからです。そして、３等分された辺はそれぞれ、小さな正三角形の一辺となっているのです。すると、右の図のような切り口であることが分かります。

　正三角形ＡＦＣは小さな正三角形９つで形成されていますね。そのうち、３つは空洞になっているわけですから、実際に切り口となっているのは６つ分です。

　というわけで、６÷９＝２/３

　　　　　　　　　　　　答え：３分の２

HELP!!はこちらへ...

masaru-y@kt.rim.or.jp

HOME