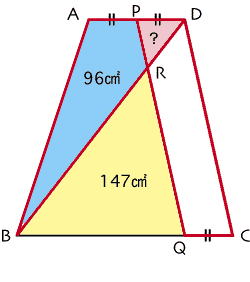
上の図をご覧ください。
三角形ABDと平行四辺形PQCDを赤線で囲んでいますが、分かりますでしょうか。(ちょっと見づらいですね...)ここで、これら2つの図形の面積を比較してみます。
ご存じの通り、三角形の面積は、底辺×高さ÷2 で求められます。
また、平行四辺形の面積は、底辺×高さ で求められますね。
ここで、上記の2つの図形を比較すると、平行四辺形PQCDは、底辺が2/1になっていることが分かります。でも、三角形と違って最後の「÷2」がありませんから、”あいこ”ですね。つまり、2つの図形の面積は等しいことが分かります。ということは、四角形RQCDの面積は96ということになりますね。
ここまできたら、あとは比較的簡単です。三角形BQRと三角形BCDは相似です。また、面積比は147:243(96+147)=49:81と分かります。よって、相似比は7:9ですね。すると今度はBR:RDが7:2であることが分かります。三角形BRQと三角形DRPは相似ですから、その面積比は49:4ということになります。
147×4/49=12
答:12