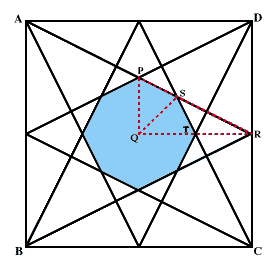
この中にできた八角形(正八角形ではありません)の面積を求めればよいことになります。
ここで、点Q,点RはそれぞれPF,FSの真ん中の点です。(図をよく見ると分かります)すると、QP:PS=1:2であることが分かりますから、三角形PSUの面積は三角形PFSの1/3であることになります。
すると....。水色の部分の面積は四角形EFGHの
1/2+1/8×1/3×4=2/3
であることが分かります。正方形EFGHは正方形ABCDの1/4の面積ですから、
36×1/4×2/3=6
答:6
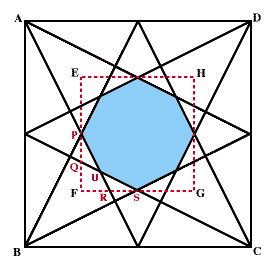
(解法その1) 下の図のように、水色の部分の周りに正方形EFGHを設定します。

この中にできた八角形(正八角形ではありません)の面積を求めればよいことになります。
ここで、点Q,点RはそれぞれPF,FSの真ん中の点です。(図をよく見ると分かります)すると、QP:PS=1:2であることが分かりますから、三角形PSUの面積は三角形PFSの1/3であることになります。
すると....。水色の部分の面積は四角形EFGHの
1/2+1/8×1/3×4=2/3
であることが分かります。正方形EFGHは正方形ABCDの1/4の面積ですから、
36×1/4×2/3=6
答:6