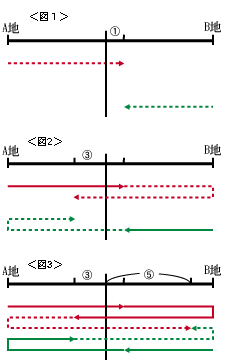
まずは、太郎君と花子さんが1度目に出会った場面を考えます。<図1>は、2人がAB間のちょうど真ん中の地点から”1”だけ離れた地点で出会ったことを示しています。(これを「半分+”1”」と表すことにします。)太郎君の方が速く歩くという設定ですから、当然真ん中の地点よりも右側で出会うことになります。
次に、2度目に出会う場面を考えます。このとき、太郎君は1回目に出会った地点から、「半分+”1”」の2倍、すなわち「半分*2+”2”」だけ歩いたことになります。つまり、出発点から測ると「半分*3+”3”」だけ歩いたことになり、2度目に出会う地点は真ん中の地点から”3”だけ左側の地点であると分かります。<図2>
最後に、3度目に出会う場合です。2度目の場合と同様に考えると、3度目に出会う地点は真ん中の地点から”5”だけ右側の地点であると分かります。<図3>
すると、1度目に出会った地点と3度目に出会った地点は、”5”-”1”=”4”だけ離れているはず。これが800mですから、”1”は800/4=200m ということになります。
よって、太郎君と花子さんの速さ比は、<図1>より、2200:1800=11:9と分かります。
2人は110分の間に合計20000m歩いたことになりますが、そのうち太郎君は、
20000*11/20=11000m
だけ歩いたことになりますから、太郎君の速さは、
11000/110=100 m/分
と分かります。
分速100m