(解法1)
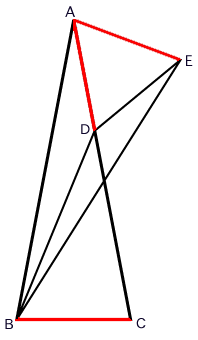
左の図で、三角形BAEは、三角形ABCと合同な三角形を作り、逆向きに重ねたものです。当然、辺ADとAEは等しくなります。また、角EADは80-20=60(度)ですから、三角形ADEは正三角形です。
すると、三角形ABDと三角形EBDは合同、ということになります。よって、角ABDの大きさは、
20/2=10(度)
であることが分かります。
(解法2)
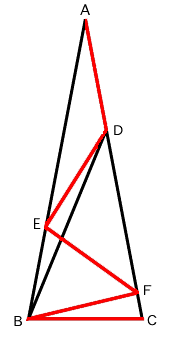
左の図のように、辺ADと同じ長さの線分を、次々にとってみます。すると、三角形ADEは底角が20度の二等辺三角形、三角形DEFは底角が40度の二等辺三角形となります。さらに続けると、点Fから出発した線分は頂点Bと重なることが分かります。(角BFCが80度になるため)ここで二等辺三角形EFBに注目すると、角BEFが180-20-100=60(度)であることから、二等辺三角形EFBは正三角形であることが分かります。
すると、三角形EBDは実は二等辺三角形であることがわかり、角ABDの大きさは、
{180-(180-20)}/2=10(度)
であると分かります。
(解法3)
下の図のように、三角形ABCと合同な三角形AEDを作ります。
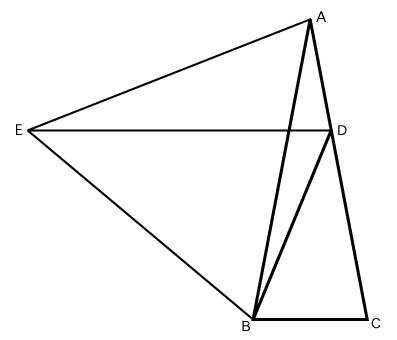
すると、AE=ABとなり、また角EABは80-20=60(度)ですから、三角形AEBは正三角形と分かります。このことから、三角形EBDはEB=EDの二等辺三角形です。角BEDの大きさは、60-20=40(度)ですから、角EBDの大きさは(180-40)/2=70(度)です。
よって、角ABDの大きさは、
70-60=10(度)
と分かります。
(解法4)
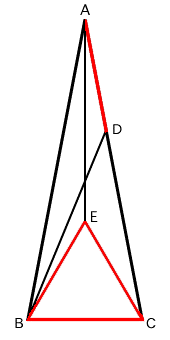
左の図のように、辺BCを一辺とする正三角形BECを作り、頂点Aと頂点Eを結びます。
ここで三角形ABDと三角形BAEに注目すると、角ABE=80-60=20(度)であることから、この2つの三角形は合同であることが分かります。(二辺とその間の角がそれぞれ等しい)よって、角ABD=角BAEですから、
20/2=10(度)
となります。
HOME




