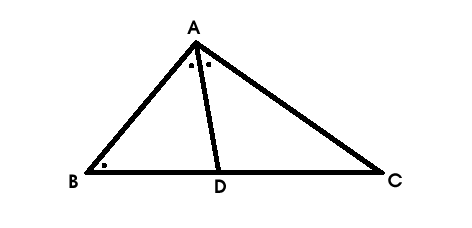
まず、頂点Aから角の二等分線をひき、BCとの交点をDとします。

そこで、三角形ABCと三角形DACを見比べると、相似であること
がわかります。(角Cが共通、さらに角ABCと角DACは等しい)
BR>
ゆえに、CDの長さをxとすると、8:6=6:xとなり、これを
解くと、CDの長さは9/2と分かります。よって、
BD=8-9/2=7/2となります。
ここで、三角形ABDは二等辺三角形ですから(理由はお分かりですね?)
ADの長さも7/2と分かります。
最後に、再び三角形ABCと三角形DACが相似であることに着目すると、
相似比を利用すればABの長さを求められることが分かります。
ABの長さをyとすると、
8:6=y:7/2、これを解くとy=14/3
答 14/3 cm